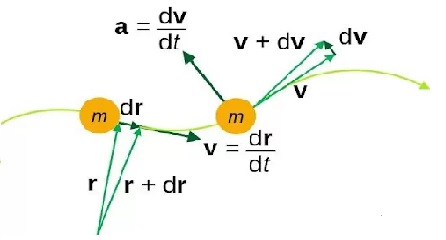
Cinemática

Cinemática do Ponto Material

<<Baseado nas notas de aula do Prof. Luiz Ferraz Netto e conteúdo da disciplina de ICF1 do IF/UFRJ>>

OBS.: Este é um texto teórico que, embora esteja acessível ao Ensino Médio, foi por mim inserido aqui para atender prioritariamente aos alunos das disciplinas introdutórias de Mecânica da Partícula dos cursos de graduação de Engenharia de Produção, Engenharia de Petróleo, Engenharia Mecânica, Eletrônica, Computação e Licenciatura em Física.

I. Conceitos básicos

01. Ponto material - todo corpo cujas dimensões relativas não interferem no estudo de determinado fenômeno.

02. Tempo - ou abscissa temporal t ou ainda 'instante t' - número real que se faz corresponder biunivocamente, mediante certas convenções, à sucessão dos eventos. À origem dos tempos (evento inicial arbitrário) associa-se, por comodidade, t = 0; aos eventos que seguem àquele tomado por O.T. associa-se t > 0 e para aqueles que o precedem, associa-se t < 0.
Intervalo de tempo Dt denota o número de unidades de tempo decorridas entre dois eventos sucessivos e calcula-se por: Dt = t2 - t1, onde t2 e t1 são os instantes associados a esses eventos.

03. Trajetória - para um dado sistema de referência, é a linha contínua S, lugar geométrico dos pontos do espaço geométrico ocupados pelo ponto material no decorrer do tempo.

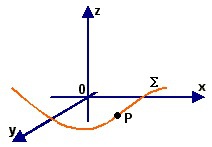
04. Espaço cinemático - posição ou abscissa linear s é o número real que se faz corresponder biunivocamente aos pontos da trajetória, mediante certas convenções (*), e que se destina a localizar o ponto sobre sua trajetória. O espaço s, só localiza (relativamente à origem arbitrária) o ponto, não indica o sentido de movimento, nem determina quanto o móvel efetivamente 'andou'.

(*) Convenções: considere sobre S o ponto arbitrário O (escolha da origem dos espaços OE) e o ponto U, de modo que a extensão do arco (OU seja adotada como unidade de medida de comprimento (exemplo, (OU = 1 m). Nessas condições, para uma genérica posição P do ponto material, s = (OP/(OU [leia-se: s é a medida do arco (OP na unidade (OU].

05. Movimento - é conceito que se define para o ponto, em relação a um dado sistema de referência. Se sua trajetória é previamente conhecida nesse referencial, o ponto se move sobre ela se sua abscissa linear s variar em função da abscissa temporal t. Isso se indica com:

s = f(t) ou s = s(t)

A expressão que associa biunivocamente a cada valor de t o correspondente valor de s [s = f(t)] é denominada 'lei de movimento', 'lei horária de movimento' ou, corriqueiramente, 'equação horária'.
Se s permanece constante (em relação a t), no referencial em questão, ele é dito em repouso.

06. Espaço percorrido - ou incremento de abscissa Ds, num dado intervalo de tempo Dt é dado por:

Dst1---t2 = s2 - s1

onde s2 é a abscissa (espaço) do móvel no instante t2 e s1 sua abscissa no instante t1.

Num dado intervalo de tempo pode-se ter: Ds > 0, Ds = 0 ou Ds < 0.

07. Velocidade escalar média - num dado intervalo de tempo, é o quociente do espaço percorrido Ds, nesse intervalo de tempo, pela correspondente extensão Dt do intervalo considerado. Esse quociente é, na matemática, reconhecido como 'razão incremental'.

08. Velocidade escalar - num dado instante t1, é o limite da velocidade escalar média definida entre os instantes t1 e t2, quando o instante t2 torna-se cada vez mais próximo de t1 (o que corresponde dizer que Dt tende para o valor zero).

Em termos de análise matemática (cálculo diferencial), sendo s = s(t) a função que associa a cada t um e um só s, a velocidade v, no instante genérico t será a derivada da função s = s(t) em relação ao tempo t e escreve-se: v = ds(t)/dt. Recomendamos, a respeito disso, a leitura Os flúxions de Newton em nossa Sala 19. A expressão v = ds(t)/dt que nos permite obter a velocidade escalar do móvel em cada instante de seu movimento denomina-se 'lei de velocidade' ou, "equação da velocidade".

09. Aceleração escalar média - num dado intervalo de tempo de extensão t2 - t1, é o quociente da variação da velocidade do móvel Dv ocorrida entre os instantes t1 e t2 pela extensão desse intervalo de tempo. Equaciona-se:
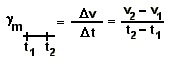